|
Автор В.В. Вычужанин, ОНМУ Системы кондиционирования воздуха (СКВ) занимают все больший процент в общем объеме капитального строительства. Растет доля эксплуатационных расходов на СКВ. В этих условиях создание экономичных и надежных систем кондиционирования — актуальная задача, решение которой существенно зависит от правильного расчета системы автоматического управления (САУ) и надежности ее элементов. Решая задачу автоматизации оборудования центральных агрегатов, в том числе воздухонагревателей, необходимо учитывать следующие рекомендации. Исследования и практика работы САУ центральных кондиционеров, построенных на устройствах, не учитывающих особенностей кондиционеров как объектов регулирования показывают, что они неработоспособны в диапазоне нагрузок 0-30% (примерно 40% времени работы в течении года) из-за нарушения устойчивости или ухудшения точности регулирования. Разработка САУ СКВ, в свою очередь, невозможна без достоверных знаний статических и динамических характеристик ее технологического оборудования, формализованного представления технологических процессов в виде математических моделей. Практика эксплуатации и проектировании автоматизированной СКВ также показала необходимость исследования и учета динамических характеристик всех звеньев системы. Критическое изучение с этих позиций схем регулирования еще на стадии проектирования уменьшает экономические расходы на аппаратуру контроля и регулирования, стоимость которой составляет значительный процент от стоимости технологического агрегата. Одним из шагов по решению задачи автоматизации СКВ является разработка математической модели статики и динамики воздухонагревателя.
Одними из основных теплообменных аппаратов, применяемых в центральных СКВ, являются воздухонагреватели. Их характеристики определяют процессы тепловой обработки воздуха в кондиционере, влияют на выбор управляющих воздействий и на качество переходных процессов в используемой САУ. Какое бы конкретное воплощение не имел любой теплообменный аппарат, он должен обладать вполне определенными статическими характеристиками, которые могут быть достаточно точно рассчитаны с помощью хорошо разработанных методов в теории теплопередач. Эти вопросы принимаются как основа для расчета динамических характеристик. Методически поставленная задача решается в таком плане, что основные теплофизические параметры и конструкция аппаратов определяются результатами расчетов статических и прочностных характеристик аппаратов, а далее, основываясь на результатах расчетов, определяются их динамические характеристики. Методы расчета стационарных режимов и общая теория стационарного теплообмена в воздухонагревателях хорошо изучена. Но этого нельзя сказать о расчете переходных процессов теплообменных аппаратов. Данные о динамических характеристиках воздухонагревателей центральных СКВ отрывочны и часто носят экспериментальный характер и обычно не учитывают связность параметров воздухообработки. Тепловые процессы, протекающие в теплообменных аппаратах, характеризуются распределенностью параметров и поэтому динамика их описывается в общем случае нелинейной системой дифференциальных уравнений в частных производных. Поэтому динамические характеристики теплообменных аппаратов можно получить, найдя распределение температур как функций пространственных координат и времени. Решение подобных задач можно получить численным интегрированием на ЭВМ или аналитическими методами. С помощью численного интегрирования поставленная задача может быть решена с очень большой точностью по исходным нелинейным дифференциальным уравнениям в частных производных. Но при таком подходе существенно возрастают затраты времени, что не всегда оправдано. Особенно в том случае, когда решение задачи выбора САУ находится в начальной стадии и требуется большой объем вариантных проработок возможных схем систем управления. Наиболее интересным является аналитическое решение. Однако, решение сложных систем уравнений в общем виде классическими методами либо вообще невозможно, либо чрезвычайно сложно и громоздко в практическом осуществлении. В силу этого при расчетах процессов в системе регулирования целесообразно в первом приближении использовать упрощенную модель объекта регулирования. Приближенные методы определения динамических характеристик теплообменных аппаратов, рассматриваемых как звенья САУ с сосредоточенными параметрами, позволяют получить решения с точностью достаточной для сосредоточенной модели вместо распределенной, что обычно подтверждается экспериментом. Точность динамических характеристик теплообменных аппаратов определяется точностью данных, полученных из расчета их стационарных режимов работы. Кроме того, известные методы возможного приближения передаточных функций к исходным, естественно, предопределяют какую-то неточность. Степень этой неточности или величина погрешности должна определяться в каждом конкретном случае опытом, заданными требованиями к показателям качества процессов всей САУ и степенью достоверности определения динамических характеристик остальных элементов, входящих в объект регулирования. Однако здесь нужно иметь в виду, что в технических задачах при математическом описании свойств практически любого объекта регулирования допускаются какие-то погрешнос ти. Это следует учитывать для правильного выбора допустимых погрешностей при аппроксимации исходных уравнений, описывающих динамику теплообмена в исследуемых аппаратах. Действительно, используя, например, метод аппроксимации с помощью интегральных оценок, можно привлекать к рассмотрению в качестве аппроксимирующих функций полиномы высокого порядка и получать достаточно высокую степень приближения. Однако при этом следует считаться с возрастающей сложностью дальнейшего решения всей задачи. Во многих случаях добиваться весьма высокой точности нецелесообразно, так как в принципе всякая задача автоматического управления в области техники решается с каким-то допустимым приближением. Операционное исчисление, основанное на преобразовании Лапласа и разработанное для исследования детерминированных дифференциальных уравнений в прикладной математике, применяется и для решения нестационарных задач теплообмена, сводящихся к определению динамических характеристик теплообменных аппаратов. Этот метод, как известно, в значительной степени основан на работах Хевисайда, Бромвича, Карслоу и Карсона и др. Рассмотрим схему парового воздухонагревателя в сосредоточенных параметрах, то есть относительно средних по тепловому балансу температур и относительной влажности воздуха на входе и выходе аппарата. В воздухонагревателях возмущающими воздействиями является температура и относительная влажность воздуха на входе ( Ä t В и Äϕ В ). Управляющими воздействиями могут быть расход пара Ä G П или температура пара Ä t П на входе, расход воздуха Ä G В (если аппарат работает при переменном расходе). Рассматривая статические и динамические характеристики теплообменного аппарата, считаем физические константы сред в рассматриваемых диапазонах изменений возмущающих воздействий неизменными. Используя известную систему уравнений, описывающих статику воздухонагревателя, определим соответствующие передаточные функции, характеризующие динамические характеристики теплообменного аппарата. Расчетные уравнения для получения и анализа характеристик рассматриваемого типового агрегата СКВ в режиме нагрева можно получить из системы уравнений теплового баланса и теплопередачи. Например, при теплоносителе паре они имеют следующий вид: 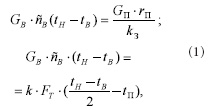
где t H , t B — начальная и конечная температура воздуха; t П — температура пара; G В и G П — расход воздуха и пара; F T — площадь теплообменной поверхности; с В — удельная теплоёмкость воздуха; r П — теплота парообразования; k З — коэффициент запаса, учитывающий неполноту конденсации пара; k — коэффициент теплопередачи парового воздухонагревателя. Система уравнений (1) может быть использована для определения статических характеристик воздухонагревателя как объекта регулирования. Уравнение статистики (1), а также преобразования Лапласа позволяют описать динамические свойства парового воздухонагревателя при ступенчатых изменениях температуры воздуха до теплообменного аппарата ( Ä t В ), расхода воздуха ( Ä G В ), пара ( Ä G П ) и его температуры ( Ä t П ). Полученная математическая модель динамики парового воздухонагревателя при ô _ 0 имеет вид: 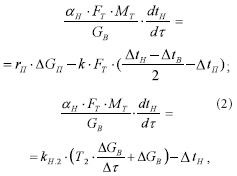
где М Т — масса теплообменного аппарата; ô — время. После соответствующих преобразований системы уравнений (2) отражающих динамические свойства парового воздухонагревателя по каналам Ä t В.2 ( р ) _ Ä t H ( р ), Ä G В ( р ) _ Ä t H ( р ), Δ t П ( р ) _ Ä t H ( р ) и Ä G П ( р ) _ Ä t H ( р ) модель аппарата имеет вид: 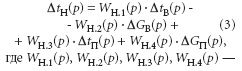
где W Н.1 ( р ), W Н.2 ( р ), W Н.3 ( р ), W Н.4 ( р ) — передаточные функции по каналам передачи возмущающих и управляющих воздействий. 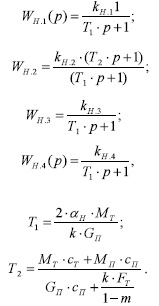
Коэффициенты передачи: 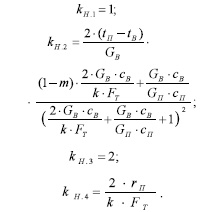
где М П — масса пара через воздухонагреватель; с Т , с П — теплоёмкость воздухонагревателя и пара; m — показатель степени критериального уравнения теплообмена. Выражения для определения постоянных времени Т 1 и Т 2 экспериментально проверены на различных паровых воздухонагревателях. Везде получена хорошая сходимость опытных данных с расчётными. Передаточные функции в уравнении (3) характерны для инерционного звена, однако подобная система может рассматриваться как состоящая из звеньев бесконечно высокого порядка (континуумы).Истинное поведение системы характеризует промежуточное состояние между инерционной системой и континуумом. При таком подходе к паровому воздухонагревателю как объекту регулирования более соответствующим представляется следующий вид передаточных функций, входящих в уравнение модели (3): 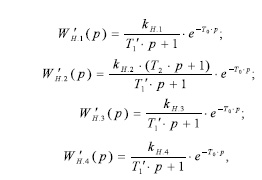
где Т ’ 1 = 0,5 . Т 1 ; Т 0 — время запаздывания воздухонагревателя как объекта регулирования ( Т 0 = 0,1 . Т 1 , с). При нагреве воздуха в воздухонагревателе помимо температуры изменяется также относительная влажность воздуха на выходе теплообменного аппарата при неизменном влагосодержании нагреваемого воздуха. Уравнение динамики, устанавливающего связь изменения относительной влажности воздуха на выходе воздухонагревателя Äϕ Н от изменений Äϕ B , Ä G В , Ä t П и Ä G П имеет следующий вид: 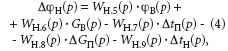
где W Н.5 ( р )… W Н.8 ( р ) — передаточные функции по каналам передачи возмущающих и управляющих воздействий; W Н.9 ( р ) — передаточная функция учитывающая связность параметров воздуха, т.е. зависимость изменения относительной влажности нагреваемого воздуха от изменения относительной температуры при нагреве воздуха. Передаточные функции, входящие в уравнение (3), определяются с учетом передаточных функций W’ Н.1 ( р )… W’ Н.4 ( р ), а также коэффициента, устанавливающего связь относительной влажности воздуха и его температуры. Модель парового воздухонагревателя в стационарных состояниях определяется из системы уравнений (3) и (4) приравниванием оператора « Р » к нулю. Разработанная модель воздухонагревателя, использовалась при исследованиях в рамках программы MATLAB 6.5 — Simulink переходных процессов изменений температуры и относительной влажности нагреваемого воздуха. Соответствующая модель приведена на рис. 1 . 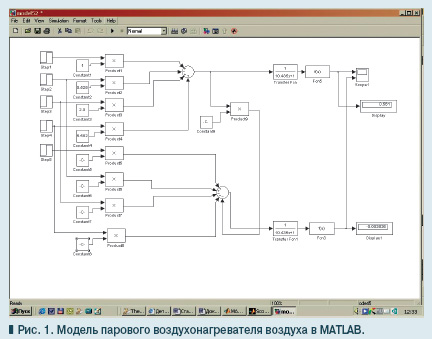
Используемые при моделировании воздухонагревателя численные значения коэффициентов передачи и постоянные времени передаточных функций, входящие в систему уравнений (3) и (4) имеют переменные значения. Они определяются с учетом расходов воздуха и пара, температуры и относительной влажности нагреваемого воздуха. Численные значения коэффициентов передачи как постоянные, так и переменные, постоянных времени переменные, так как они определяются с учетом характера решаемой задачи в СКВ, расходов воздуха и пара, температуры пара, температуры и относительной влажности нагреваемого воздуха. Расход воздуха в «зимнем» периоде работы СКВ считается постоянным, равным минимально необходимому, обоснованному санитарными нормами в зависимости от термодинамического состояния, газовой нагрузки и поставленных задач обеспечения комфортного микроклимата в помещениях и минимизации энергозатрат в СКВ. Расход пара переменный, изменяющийся в установленных каталожными данными диапазоне. На рис. 2 приведены результаты моделирования исследуемого объекта, отражающие его динамические свойства, при подаче соответствующих возмущающих и управляющих воздействий ступенчатого характера на соответствующие входы модели. 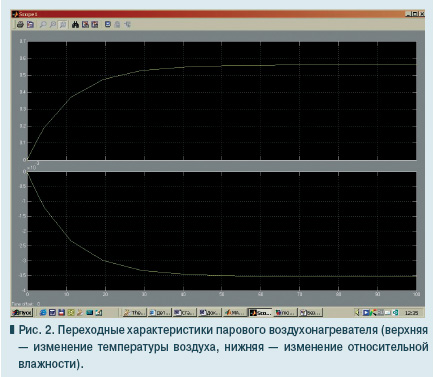
Полученная математическая модель парового воздухонагревателя, а также результаты исследования его динамики отражают реальный характер изменений параметров нагреваемого воздуха и могут быть использованы при разработке и эксплуатации устройств для СКВ, обеспечивающих качественный автоматический режим нагрева воздуха. ■ |









